​ 这个题是一个数学题，主要的知识点是组合数学相关的内容，在高中阶段，大家学习过一些组合数学相关的知识。通过对题目进行分析，由于题目说明了每位同学最多只有一个时段不能来实验室值班，且各个时段互不冲突，故每位同学具体在哪个时间段不能在哪个时间段来值班是不会对结果造成影响的。故该问题可以等价为每名同学有一个时段不能来实验室，且时段均不冲突。由此，该问题可以简化成为第i位同学不能在第i个时间段来实验室值班，一共有多少种不同的安排方案。

​ 解决这个问题的方法是采用容斥原理的思想。首先不考虑冲突的情况，即n个元素的全排列。之后，考虑会发生冲突的情况。先考虑时段1，时段1不能够安排第1位同学值班，我们把全排列中，时段1为1的同学的所有情况都去掉，同理，对n个同学都采用这样的操作，这时，由于在统计第1个同学的时候，会同时统计到第2个同学的情况。例如：1 2 3 4 5这种，在统计到时间1和2的时候都会统计到它。于是我们需要利用容斥原理进行一个去重。将这种情况加回来。而一共有多少种重复的方案数呢？通过容斥原理我们知道，同时取到1和2的时候就会重复计算，这时，我们就需要把这些重复的元素去掉。就拿1、2同时选择的情况来说吧，会出现这种情况的可能是(n-2)!。一共有C(n,2)*(n-2)!种情况，这次在去掉的时候，会将同时选择1，2，3的情况在选择1，2和2，3的时候去掉，这时，我们就要把这种情况又加回来，一共是C(n,3) *(n-3)!种情况。以此类推，便可以得到下列的公式：

$$ANS=A(n,n)+(-1)^1C(n,1)*A(n-1,n-1)+(-1)^2C(n,2)*A(n-2,n-2)+(-1)^3C(n,3)*A(n-3,n-3)+……+(-1)^(n-1)*C(n,n-1)*A(1,1). $$

编程求解该公式即可。

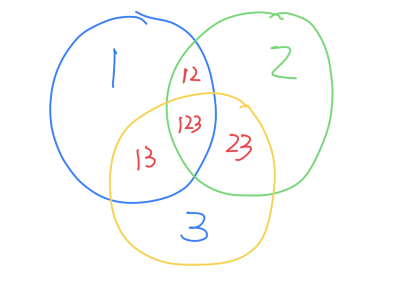
上述重复计算的部分示意图。S=1+2+3-12-13-23+123。

参考代码：

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n,m,i,j;
	long long ans=1;
	cin>>n>>m;
	for (i=1;i<=n;i++)
	{
		ans=ans*i;
	}
	for (i=1;i<=m;i++)
	{
		int s1,s2;
		cin>>s1>>s2;
	}
	int tmp=0;
	for (i=1;i<=m;i++)
	{
		long long sum=1;
		for (j=1;j<=(n-i);j++)
		{
			sum=sum*j;
		}

		for (j=m;j>m-i;j--)
		{
			sum=sum*j;
		}
		for (j=1;j<=i;j++)
		{
			sum=sum/j;
		}
		if (tmp==1)
		{
			ans=ans+sum;
			tmp=0;
		}
		else
		{
			ans=ans-sum;
			tmp=1;
		}
	}
	cout<<ans<<endl;
	return 0;
}