1 solutions
-
2
1.题目描述
有n种纪念币,每种纪念币被买到的概率为, 特别的,第k次购买花费k元,问期望花费是多少?
2.思路
①令f[i]表示买了i种纪念币购买的次数
②令g[i]表示买了i种期望的花费
③计算得到的g[n]代表买完的花费,即为结果
3.易错点
①我们可能会重复购买纪念币,不要单单以为买了一种纪念币,下一次就买不到了。
②第k次购买,k元,是针对每一种邮票,而不是我买了一个新的,还是k+1,买了一个新的,就又重新从1开始。
4.具体分析
显然f[0]=g[0]=0
4.1、
我们要求第i种纪念币的期望购买次数,即我们已经购买了i-1种纪念币,我们有x=的概率买到已经买到的,有y=1-=的概率买到没有的。
我们买第一次,就可以买到下一个纪念币的概率为:
我们买第两次,就可以买到下一个纪念币的概率为:
我们买第三次,就可以买到下一个纪念币的概率为:
我们买第四次,就可以买到下一个纪念币的概率为:
以此内推......
我们买第k次(假设k为正无穷次),就可以买到下一个纪念币的概率为:(这里代表的是x的k-1次方乘以y,由于Markdown写不出来,就这样写了)
下一步,我们把它累加起来,上图:
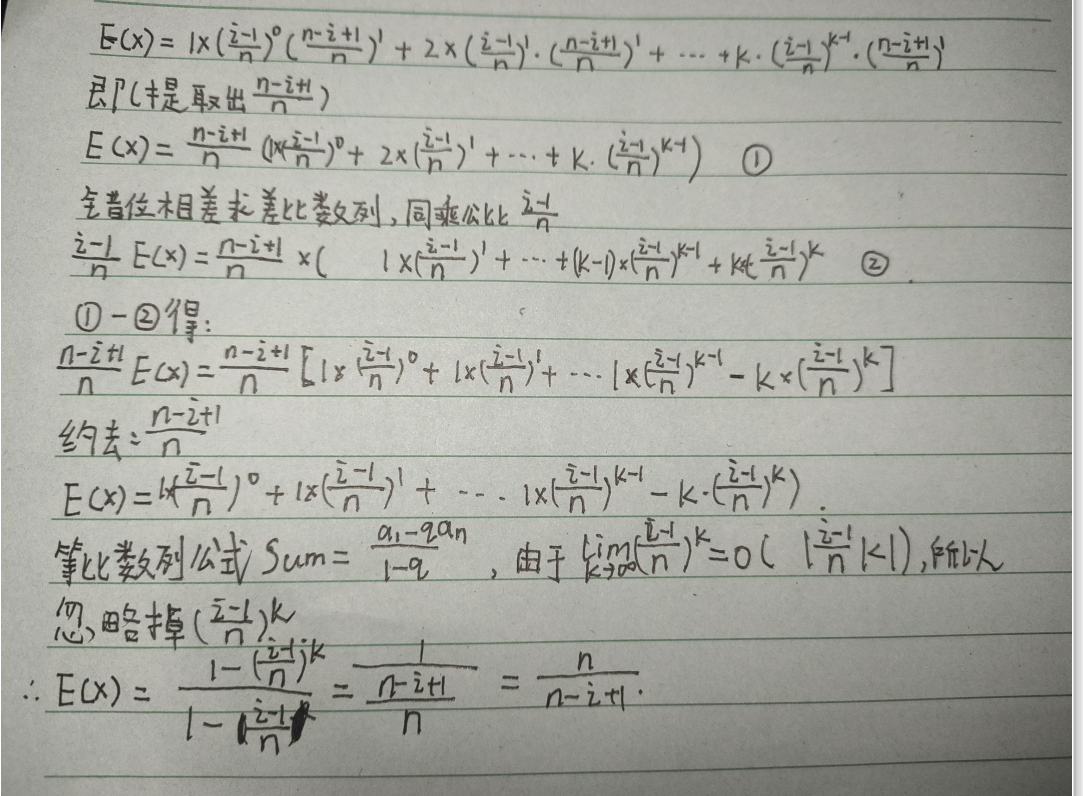
于是我们代回原数据:
4.2、
下面给出的递推式:先理性感受一下
下面给出推到过程:
我们已经买了i-1种纪念币,已经买了次
我们再买一次就买到没有买过的纪念币、花费为元,期望花费就是$(x代表的是(i-1)/n,y代表的是(n-i+1)/n别忘了,忘了的可以看看上面的x,y是什么意思)$
我们再买一次就买到没有买过的纪念币、花费为元,期望花费就是
我们再买一次就买到没有买过的纪念币、花费为元,期望花费就是
再买k次(假设k为正无穷次)花费为:,期望花费就是(这里代表的是x的k-1次方乘以y,由于Markdown写不出来,就这样写了)
下一步,我们把它累加起来,上图:

继续求S1,S2

所以我们得到
因为
所以
讲带入,上图:
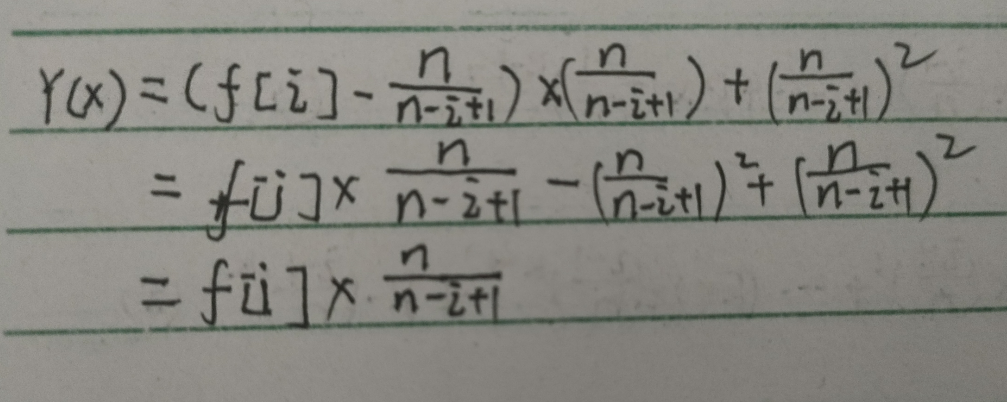
所以我们就得到了:
于是这道题就做完了
AC代码:
#include<iostream> using namespace std; int n; double f[10005], g[10005]; signed main() { scanf("%d", &n); g[0] = 0; f[0] = 0; for (int i = 1; i <= n; i++) { f[i] = f[i - 1] + (n * 1.0) / (n - i + 1); g[i] = g[i - 1] + f[i] * n * 1.0 / (n - i + 1); } printf("%0.2lf\n", g[n]); return 0; }5.反思总结
①这道题考察的是数学功底
②考察细心和耐心
- 1
Information
- ID
- 6610
- Time
- 1000ms
- Memory
- 256MiB
- Difficulty
- 8
- Tags
- (None)
- # Submissions
- 22
- Accepted
- 6
- Uploaded By
