You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

Description

A standard sphere ball is falling in the air, and the center of the sphere is exactly on the centerline of an empty isosceles trapezoidal. The trapezoid is hanging horizontally under the sphere.

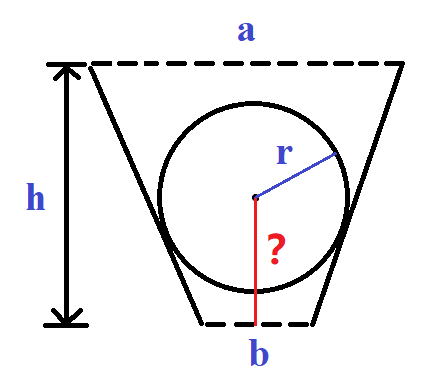
Please determine whether the ball will get stuck in the trapezoid or drop past the trapezoid.

Input

The input contains four integers r, a, b, h$(1 \le r,a,b,h \le 1000, a > b)$, indicating the radius of the ball, the top base, the bottom base, and the height of the isosceles trapezoid.

It is guaranteed that $2r \ne b, 2r < a, 2r < h$ ​

Output

Output 'Drop' if the sphere ball will drop past the empty trapezoid, otherwise output 'Stuck'.

If the answer is 'Stuck', please also calculate the stuck position(the height between the center of the sphere and the midpoint of the bottom base). please output remain ten point

Samples

2 8 2 5

Stuck
2.2206345966

1 8 3 5

Drop

Limitation

1s, 1024KiB for each test case.