经典的尼姆博弈

吃面包一共就三种情况

n=1：先吃面包，先手必胜。

n=2：有俩种情况：

1.（m，m）型： 按照“有一学一，照猫画猫”法，先手必输。

2.（m，M）型： 先手先从多的一堆中吃掉(M-m)个，此时后手面对(m,m)的局面先手必胜。

n=3：

1.（m，m，M）型： 先手必胜局，先手可以先吃M个，之后就变成（m，m，0）的局面，也就是上述n=2的局面。

2.（a1，a2，a3）型： 举个例子(1,2,3),先手吃完之后可能的局面为(0,2,3),(1,1,3),(1,0,3),(1,2,2),(1,2,1),(1,2,0)都是之前讲过的，情况如下：

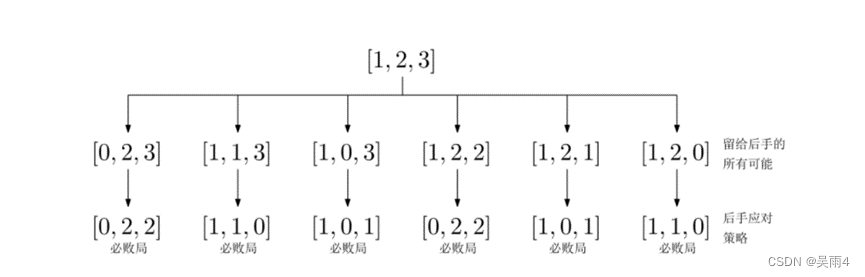
总结下来规律就是：异或结果均为0。（不懂异或结果的建议百度）

n>3的情况依次推理。

获胜情况的讨论

异或结果为0，后手必胜。

异或结果不为0，则先手必胜。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+15;
ll n,a[N];
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=0;i<n;i++)
		cin>>a[i];
	int ans=a[0];
	for(int i=1;i<n;i++) ans^=a[i];//^就是做异或运算
	if(ans==0) cout<<"女士优先，您请。"<<endl;
	else cout<<"这面包这么多，我先吃！"<<endl;
	return 0;
}